Introduction

Jules Verne was one of the first novelists to bring science and mathematics into literature. But he was not a mathematician. Despite his meticulous research and the assistance he asked of experts, mathematical errors often pop up in his works, for various reasons.

In Hector Servadac, for instance, the period of the comet Gallia’s orbit is much shorter than it should be based on its perihelion and aphelion (Crovisier 2005). Even if Verne was aware of this, it was a narrative necessity to ignore Kepler’s law in this case, as he could not have his heroes spend several years in the cold outer regions of the solar system. As another example, the cryptoanalysis described in La Jangada is faulty in several respects, clearly a result of Verne’s own imperfect understanding of the field (De Vries-Uiterweerd, in preparation). And of course, Verne’s works are full of the simple errors in transcription, chronology and unit conversions that even the cleverest mathematician might commit.[1]

In the case of Mirifiques aventures de maître Antifer (hereafter abbreviated as MA), an original and captivating novel about a treasure hunt along various portions of the globe, whose plot revolves around a bit of mathématique amusante, a mathematical inaccuracy provides an interesting clue regarding the method that Verne used for his calculations. This article will describe the spherical geometry behind the plot, and show why Verne’s results were off.[2]

Synopsis of the novel

For a better understanding of the following discussion, a brief synopsis of the novel is in order.

Captain Antifer receives a strange inheritance: the latitude and longitude of an island in the Imamate of Muscat, where the wealthy Egyptian nobleman Kamylk-Pacha buried an enormous treasure (MA 1, ch. V–IX). On this island, however, he only finds another longitude, to be combined with the latitude that is in the possession of a second heir (MA 1, ch. XVI). The two legatees travel to Mayumba Bay, only to find yet another longitude, which, when combined with the third inheritor’s latitude, leads to an island in the Spitsbergen archipelago (MA 2, ch. X–XIII). And once again, this island does not contain the treasure, but only a document giving directions to find the fourth and final island, which is located at the centre of the circle formed by the three islands already visited:

The three islands are situated on the circumference of the same circle. Well, let us assume that they all lie in one plane, join them pairwise by a straight line […] and draw a perpendicular line through the midpoint of each of these two lines… These two perpendicular lines will meet at the centre of the circle, and at this central point […] the fourth island must by necessity be located!

[Les trois îlots sont situés à la circonférence d’un même cercle. Eh bien, supposons-les tous les trois dans un même plan, réunissons-les deux à deux par une ligne droite […] et élevons une perpendiculaire au centre de chacune de ces deux lignes… Ces deux perpendiculaires se rencontreront au centre du cercle, et c’est à ce point central […] qu’est nécessairement situé l’îlot numéro quatre!] (MA 2, ch. XV)

Antifer’s nephew Juhel takes his globe and determines the centre of this circle: 37° 26′ N, 10° 33′ E.[3] Antifer and his friends set sail to this position, but no island, however small, is to be found. Then comes the revelation: Kamylk-Pacha buried his treasure on the volcanic island Julia, which had appeared in these waters on 28 June, 1831, and disappeared again in December of the same year, taking the treasure with it to the bottom of the sea (MA 2, ch. XVI).

Validity of the method described by Verne

It is useful to investigate in some detail how Juhel determines the coordinates of the fourth island:

Juhel placed the globe in the middle of the table. With a flexible ruler and a ruling pen in his hand, as if he worked on a flat surface, he drew a line between Muscat and Mayumba, and another line between Mayumba and Spitsbergen. Through the respective midpoints of each of these two lines he drew two perpendicular lines, which intersected precisely at the centre of the circle.

[Juhel plaça le globe au milieu de la table. Une règle flexible et un tire-ligne à la main, comme s’il eût opéré sur une surface plane, il joignit par une ligne Mascate à Ma-Yumba, et par une seconde ligne Ma-Yumba au Spitzberg. Sur ces deux lignes, en leur milieu respectif, il éleva deux perpendiculaires, dont le croisement s’effectua précisément au centre du cercle.] (MA 2, ch. XV)

In a plane, the problem is straightforward, and the centre of a triangle’s circumcircle (called the circumcentre) can be found as described by Verne (see Fig. 1).[4] In three-dimensional space, where the three islands lie on the surface of a sphere, matters are not that simple.

 

 

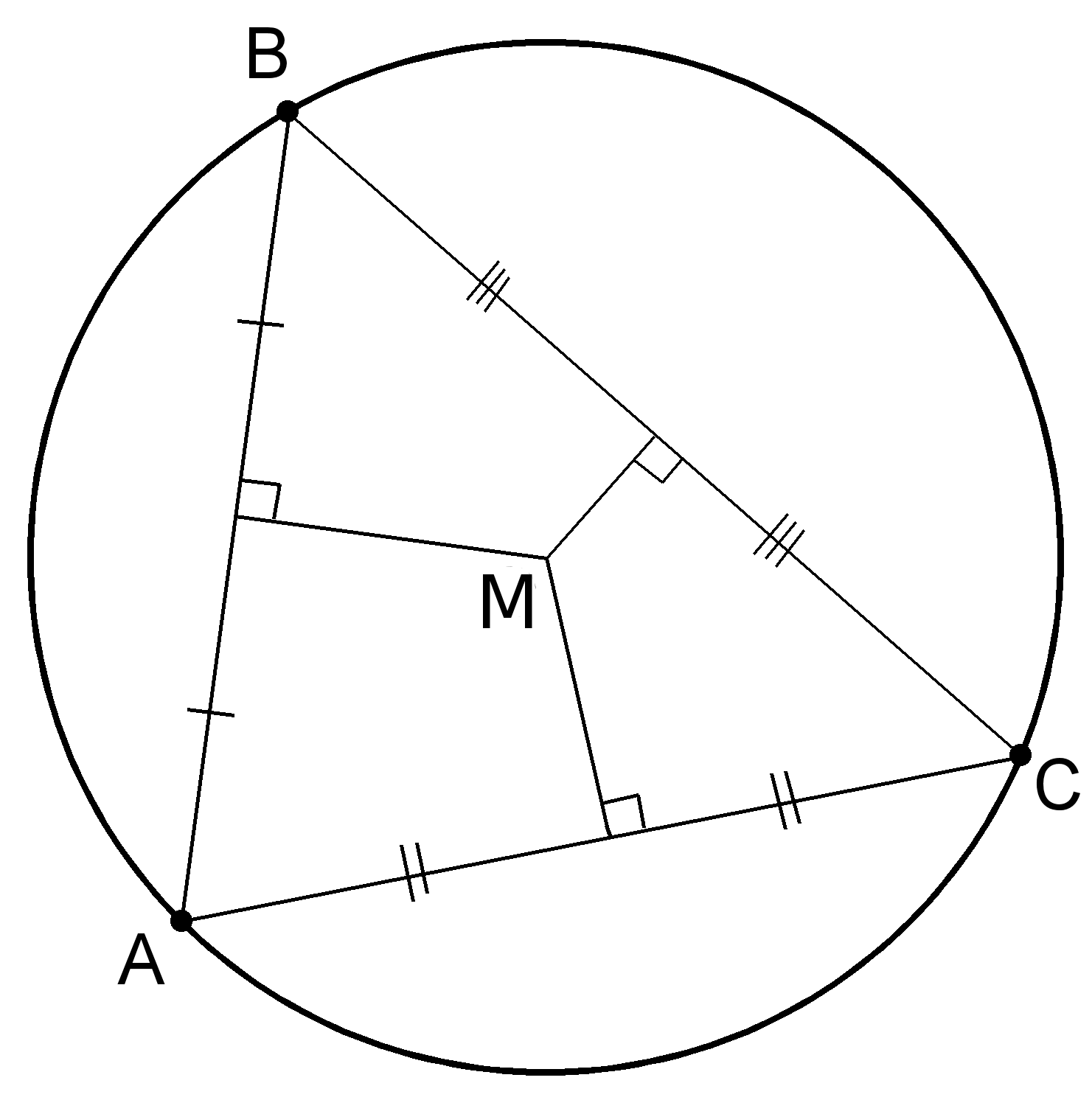
Figure 1. Construction of a triangle’s circumcircle in a plane.
All points on the perpendicular bisector of AB are equidistant to points A and B,
and all points on the perpendicular bisector of BC are equidistant to points B and C.
Hence, the intersection of these lines has equal distance to points A, B and C and is therefore
the circumcentre of the triangle.

 

Of course, the three points lie on a uniquely defined circle, but whereas this circle lies entirely on the Earth’s surface (it is the intersection of the sphere with the plane defined by the three points), its centre lies below the surface, as do the lines between the points (see Fig. 2). Because the treasure island does not lie deep underground, the problem must be solved on the surface.

 

 

Figure 2. The three islands and their circumcircle.
O denotes the centre of the Earth, P is the North Pole.
Point M′ is the (subterranean) circumcentre of the islands at A, B and C.
Point M is the location of the fourth island, directly above M′.

 

Many well-known theorems from two-dimensional Euclidean geometry do not apply on a curved surface like the surface of the Earth. For instance, the sum of the angles in a triangle on a sphere is always larger than 180° and parallel lines do not exist. It is not a priori evident that on a curved surface the circumcentre of three points can be found by the same method as in a plane.

Rather than by a straight line, each pair of islands must be connected by an arc of a great circle in order to operate entirely on the Earth’s surface. A great circle (a circle whose centre lies at the centre of the Earth) is the spherical equivalent of a straight line in a plane: a segment of a great circle is the shortest path between two points. The perpendicular bisectors of these arcs between the pairs of islands, again drawn along great circles, do indeed intersect in one point, which is equidistant to each of the islands (see Fig. 3).

 

  

 

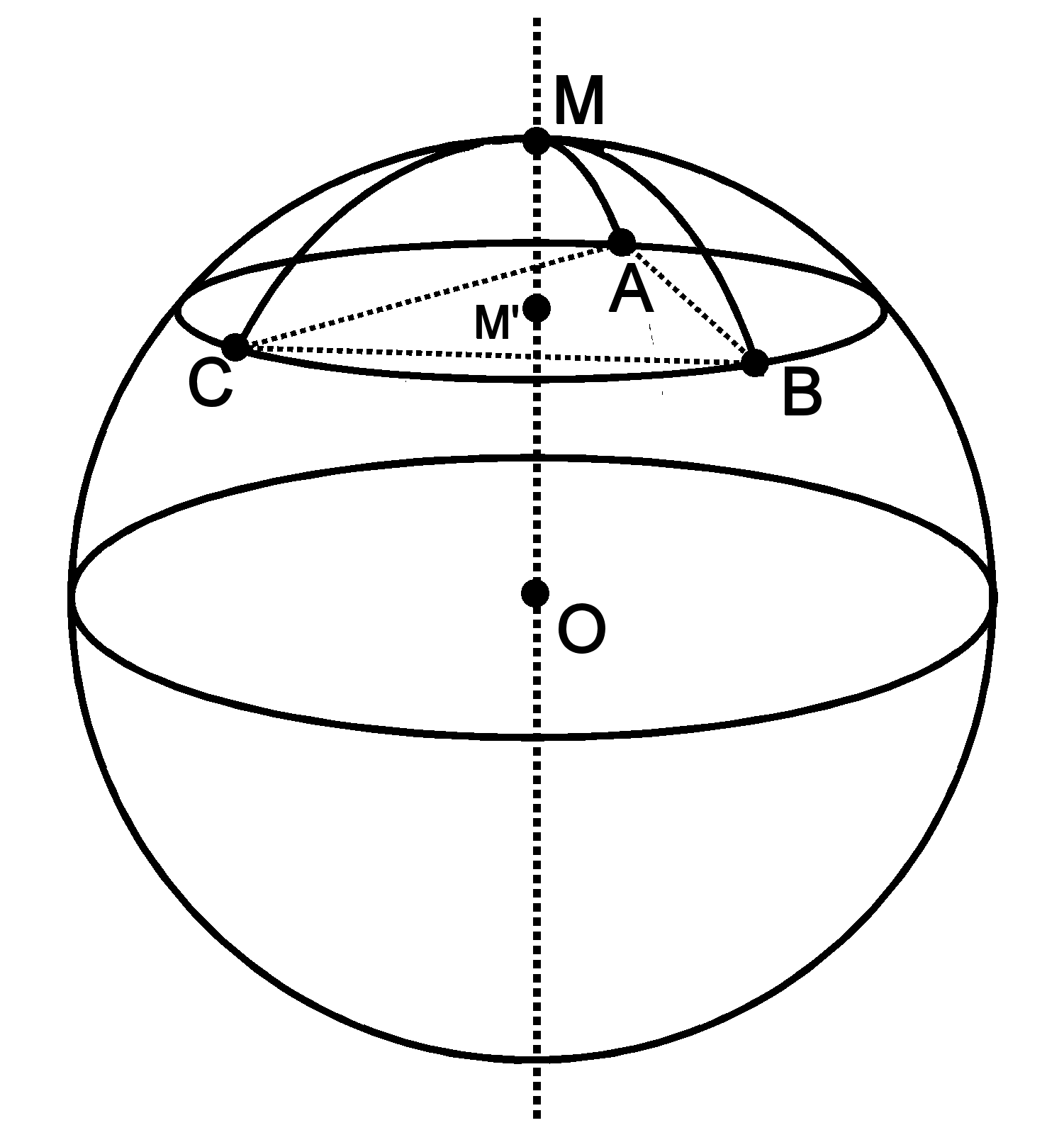
Figure 3. Construction of a triangle’s circumcentre on a sphere. The Earth as represented in Fig. 2 is rotated,
such that the points A, B and C lie on a parallel (left). The point M′, the centre of this parallel,
lies on the sphere’s axis. The point M lies directly above M′, i.e. at the new pole. Hence, it lies
at equal distances from each of the three points and is therefore the circumcentre of A, B and C on the surface
of the sphere. The sphere is then rotated around its new polar axis until A and B lie at equal distances
from the prime meridian (right). From the symmetry of the situation (invariance under reflection in the plane
defined by the prime meridian), it is clear that the prime meridian intersects the arc AB of the great circle
through A and B perpendicularly in its middle. A similar argument applies to BC and AC. Since all meridians
intersect at the pole, M is indeed the intersection of the perpendicular bisectors of the arcs connecting the islands.

 

Although Juhel’s method is theoretically correct, it must be pointed out that in practice it is not as accurate as suggested by Verne’s description:

And having carefully determined the meridian and the parallel, he pronounced firmly:

“Thirty-seven degrees twenty-six minutes North, and ten degrees thirty-three minutes East of the Paris meridian.”

[Et, après avoir relevé avec soin le méridien et le parallèle, il prononça d’une voix ferme:

«Trente-sept degrés vingt-six minutes de latitude nord, et dix degrés trente-trois minutes de longitude à l’est du méridien de Paris.] (MA 2, ch. XV)

It is not easy to draw a line through the exact centre of an arc, exactly perpendicular to it and lying exactly on a great circle. Deviations are inevitable. We will assume that the globe used by Juhel has a radius of about 20 cm, as depicted in the illustration by George Roux (see Fig. 4). The mean radius of the Earth is 6,371 km. Hence, any deviation in Juhel’s construction of the circumcentre and the reading of its coordinates on his globe is magnified with a factor 6,371,000:0.2, or almost 32 million, when applied to the real surface of the Earth. A deviation of 1 mm on the globe becomes an error of 32 km in reality. It is impossible to read the island’s coordinates to an accuracy of one arc minute, which would correspond to 0.058 mm on the globe—the thickness of a human hair!

 

 

Figure 4. Juhel and his globe. (Illustration by George Roux.)

 

Determination of the circumcentre using vector algebra

A better solution would be to use an exact formula, as can be derived from spherical geometry. Juhel might have been able to perform this kind of calculation, as he is an experienced sailor, and “he was not deficient in either practice or theory [ni la pratique ni la théorie ne lui manquaient]” (MA 1, ch. IV).

Consider again the three points A, B and C in Fig. 3. The points define a plane parallel to the equator. The lines connecting the points also lie in this plane. The line OM through the centre of the Earth and the pole is perpendicular to the equator and therefore to the plane through A, B and C. A well-known theorem states that any line that is perpendicular to two intersecting lines is perpendicular to the plane defined by those lines. Hence, the line through O perpendicular to AB, BC and AC intersects the Earth’s surface at M. This line can be found using simple vector algebra.

Each point on the Earth’s surface can be represented by a vector whose origin is at the Earth’s centre; a line between two points can be represented by the difference between two vectors. The cross product μ of b–a and c–b (see Fig. 5) equals:

μ = (b–a) × (c–b) = b×c – b×b – a×c + a×b = a×b + b×c + c×a (1)

 

 

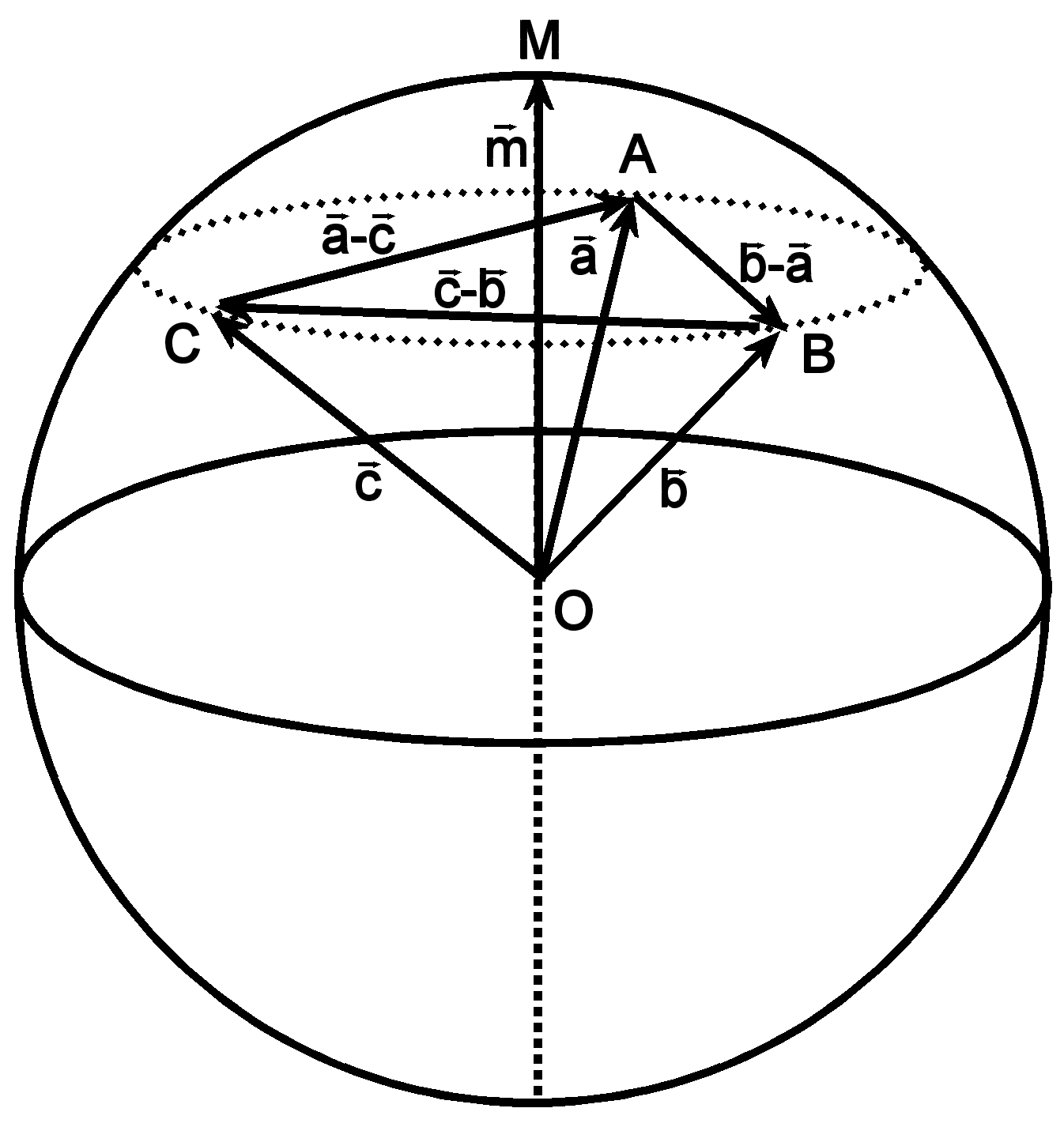
Figure 5. Points on a sphere, represented by vectors.
Vector a points from O to A, vector b from O to B, etc.
Furthermore, b–a points from A to B, etc.

 

It is perpendicular to both b–a and c–b and therefore points towards the North Pole. This means that, up to a normalisation factor, which does not affect its direction, μ is equal to the vector m pointing from O to M, the circumcentre of A, B and C. Note the invariance of this expression under permutation of a, b and c, which is a result of the fact that the order in which the three islands are visited is irrelevant.

Substitution of the positions of the three islands in Muscat (24° 59′ N, 54° 57′ E), Mayumba (3° 17′ S, 7° 23′ E) and Spitsbergen (77° 19′ N, 15° 11′ E) into Eq. 1 yields the coordinates of M: 37° 02′ N, 9° 30′ E (see Fig. 6). The steps involved in this rather straightforward calculation are detailed in the Appendix, for the benefit of the reader who wishes to follow them one by one.

 

 

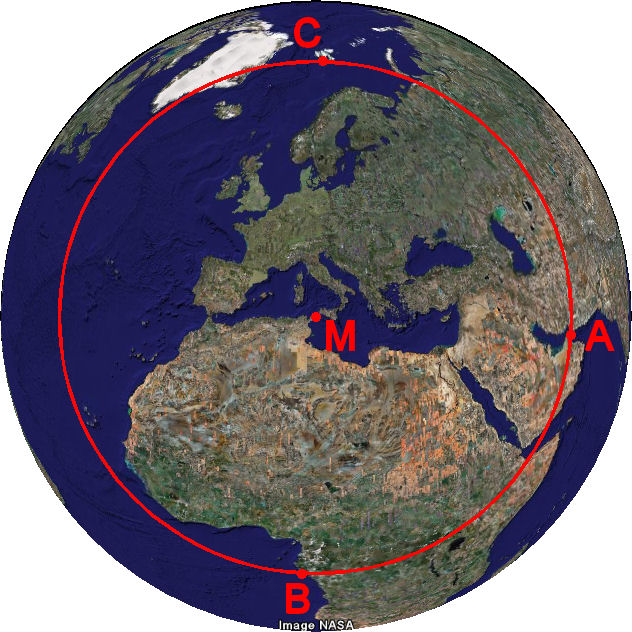
Figure 6. Azimuthal projection of the Earth, with the three islands
at points A, B and C and the island Julia at the pole M.

 

Deviation of Verne’s result from the exact calculation

The result as found by means of exact equations differs slightly from the position found by Juhel: 37° 26′ N, 10° 33′ E. The difference is 0.93°, corresponding to a distance of 103 km.[5] On a globe with a radius of 20 cm, the error would be 3.2 mm. From this discrepancy, some conclusions can be drawn regarding the method used by Verne to reach his result.

It is clear that calculations based on vector algebra were beyond Verne’s own capabilities. The possibility that Verne consulted a mathematician, like he did for earlier novels such as De la Terre à la Lune or Sans dessus dessous, can also be ruled out. A mathematical expert would have used the method outlined above (or an equivalent method) and arrived at the correct result. A truly skilled mathematician might have taken into account the fact that the Earth’s surface is not a sphere but approximately an ellipsoid. The mathematics of ellipsoidal geometry were known at the time. However, calculating distances on an ellipsoid requires the use of iterative methods, and an analytical expression corresponding to Eq. 1 cannot be found. It is unlikely that anyone would have taken all this extra trouble. Besides, the effect of the Earth’s non-spherical shape is small (it only causes an error of 19 km in the calculation of Julia’s position) and cannot explain the discrepancy.

It is worth noting at this point that Jules Verne’s brother Paul, who, like Juhel, was a sea captain, proofread the novel, mainly the “hydrographic” aspects (Dumas 1988, p. 464). Spherical trigonometry is an integral part of a sea captain’s education, even though in everyday practice one tends to apply a limited set of well-known formulae, rather than to derive algebraic expressions from scratch. Many officers may lack the mathematical skills for such an active use of trigonometry. But Paul Verne had been educated at a high-level, and he had been an officer in the Marine Impériale; he would probably been capable of performing the sort of calculations outlined above. He yet apparently accepted the numbers as given in the novel and did not suggest the use of an exact formula. He may have realised that such precision was not needed for the story and that the geometric construction on a globe was more illustrative, or he may simply have been swept along by the narrative without considering the precision of Juhel's method.[6]

Since no algebraic calculations were used, Verne must have employed some geometric construction method, either on a (two-dimensional) map or on a (three-dimensional) globe. In general, cartographic projections distort angles, distances and/or directions on the Earth’s surface. If Verne had reconstructed the circumcentre on a flat map, this would most probably have been a map which, like the one used by Antifer, “was drawn according to Mercator’s planispheric projection [était dressée d’après la projection planisphérique de Mercator]” (MA 1, ch. IV). On such a map, with its large distortions at high latitudes, the circumcentre as determined by plane geometry would be located in the North Sea, almost 2000 km from Julia’s true position, due to the third island, Spitsbergen, which lies at 77° 19′ N.

The most likely possibility is that Verne did in fact work with rulers and pens on a globe, just like Juhel does in the novel. The inaccuracy inherent to this approach explains the deviation in Verne’s results quite well. One might even expect a larger error than only a few millimeters on the globe’s surface.

Obviously, Verne did not determine the circumcentre from the positions of the first three islands. He chose the island Julia first, as he needed its brief existence for the final plot twist. He probably took a compass and drew a circle around this island, running through some interesting parts of the world, and picked the coordinates of the three islands such that they lay on the circle. Reading off the coordinates is slightly easier than reconstructing a circumcentre, since it does not involve drawing perpendicular bisectors and determining their intersection (an exercise Verne may or may not have done to verify his result). Still, Verne’s results are remarkably accurate, considering he suffered from bad eyesight and writer’s cramp at the time when he wrote Mirifiques aventures de maître Antifer.

Conclusions

From the spherical geometry behind the plot of Mirifiques aventures de maître Antifer, it can be shown that Verne did in fact use the method he describes in the novel, drawing lines on a globe rather than calculating the circumcentre algebraically. His results, corresponding to a deviation of 3.2 mm on a globe with a radius of 20 cm, are quite good, although the deviation of 103 km on the surface of the Earth is too large for the method to be of use in a real-life treasure hunt.

Works cited

Crovisier, Jacques. “Hector Servadac (1877) et les comètes de Jules Verne.” Astronomie 119 (2005): 234–239.

De Vries-Uiterweerd, Garmt. “Meetkunde op een boloppervlak.” De Verniaan 42 (2008): 12–17.

De Vries-Uiterweerd, Garmt. “Où il est question de chiffres. The cryptogram in La Jangada.” In preparation.

Dumas, Olivier. Jules Verne. Lyon: La Manufacture, 1988.

Verne, Jules. De la Terre à la Lune. Paris: Hetzel, 1865.

Verne, Jules. Hector Servadac. Paris: Hetzel, 1877.

Verne, Jules. La Jangada. Paris: Hetzel, 1881.

Verne, Jules. Sans dessus dessous. Paris: Hetzel, 1889.

Verne, Jules. Mirifiques aventures de maître Antifer. Paris: Hetzel, 1894.

Notes

1. Uniquely, an error made by J.T. Maston in Sans dessus dessous is in fact a major plot point, only to be revealed at the end of the novel. The correct calculations are given in an appendix by Albert Badoureau, Verne’s advisor for this novel. ^
2. The mathematical concepts behind the plot of MA were discussed in an earlier article by the author (De Vries-Uiterweerd, Garmt. “Meetkunde op een boloppervlak.” De Verniaan 42 (2008): 12–17.2008). ^
3. All longitudes given in this article are relative to the meridian of Paris, as in the novel. ^
4. All figures, except the original illustration from the novel, were created by the author. ^
5. The position of the island as given by Verne differs both from the exact circumcentre of the first three islands and from the Julia island’s true position, 37°06′ N, 10°22′ E. It is important to distinguish these deviations. The first is a result of Verne’s inaccurate determination of the circumcentre, the second is probably due to an error in Verne’s sources or imprecise measurements of the island’s position during the few months of its existence. ^
6. Thanks to Bernhard Krauth and Philippe Valetoux for sharing their experience and their opinions on this topic.^

Appendix

The following outline will allow the interested reader to repeat the calculations that lead to the determination of the circumcentre of three points a, b and c on the Earth’s surface.

1. Convert all latitudes and longitudes into decimal numbers.

2. Convert the positions of the three points from spherical to Cartesian coordinates:

   x = R cos(θ) cos(φ) (2)

   y = R cos(θ) sin(φ) (3)

   z = R sin(θ) (4)

   where R is the average radius of the earth, θ is the latitude and φ is the longitude.

3. Determine the cross product a×b, given by:

   a×b = (a_yb_z–a_zb_y, a_zb_x–a_xb_z, a_xb_y–a_yb_x) (5)

   and similarly for b×c and c×a.

4. Add a×b, b×c and c×a to find m.

5. Convert back to spherical coordinates:

   ρ = √(x²+y²+z²) (6)

   θ = arcsin(z/ρ) (7)

   φ = arctan(y/x) (8)